AZIMUT DE UNA PARED

AZIMUT DE UNA PARED

  Un método experimental sencillo.

   Construyendo relojes de Sol.

Cuando se quiere trazar un reloj de Sol en una pared, surge inmediatamente el problema de la orientación de la pared con respecto al meridiano.

Por norma, aunque parezca pesimista, el muro que se escoja para colocar un reloj de Sol de cuadrante vertical no estará en escuadra con el meridiano del lugar de manera que la superficie de la misma quede de lleno hacia uno de los polos geográficos, circunstancia que nos obliga a diseñar un reloj Solar Vertical de cuadrante Declinante.

Es de vital importancia para el buen funcionamiento del reloj Solar Vertical Declinante conocer la orientación de la pared con respecto a la línea meridional, el ángulo formado por un plano imaginario normal (perpendicular)  a la superficie de la pared con el plano meridional del lugar se le conoce como azimut (acimut) de la pared.

Existen varios métodos para determinar el ángulo azimut de la pared que queremos utilizar para nuestro proyecto Solar, unos más complejos que otros, unos más exactos que otros. En esta entrega nos dedicaremos a la fabricación de un pequeño instrumento que nos permitirá determinar indirectamente por medio del cálculo y de la observación el azimut de una pared con la suficiente exactitud para los relojes solares caseros.

En la red podemos encontrar un método simple que utiliza una plomada como elemento indicador, su inconveniente es que funciona solamente para la condición de que el Sol de de lleno en la pared, tomándose la hora en que esto ocurre y de allí se deduce el acimut de la pared que es la del Sol para ese momento, si el Sol no llega a enfrentarse de lleno a la pared este método no puede utilizarse.

El esquema siguiente muestra el aspecto físico del instrumento propuesto para deducir el ángulo acimut de la pared.

El instrumento se asemeja bastante a un reloj de Sol de cuadrante Polar.

Este instrumento posee un indicador (nomon) perpendicular al plano soporte, sobre el cual hay una graduación milimétrica cuyo objetivo es la de permitirnos medir con cierta exactitud la longitud de la sombra proyectada del indicador sobre el plano graduado. Para garantizar la verticalidad requerida para la medición, el instrumento cuenta con una plomada adosada al canto del indicador, de manera que cuando el canto del indicador y el hilo de la plomada coinciden, el indicador está en la vertical requerida.

Aunque la idea es simple, para deducir el azimut de la pared tenemos que conocer aparte de la longitud de la sombra del indicador, la declinación del Sol para el día de la medición, la latitud del lugar, la hora solar local deducida de la hora legal y la Ecuación del Tiempo. Con esta información a mano es posible calcular el azimut del Sol, del cual se deduce el de la pared.

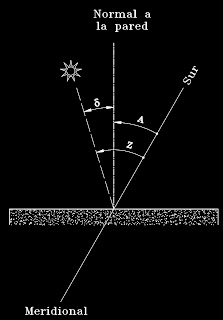
La figura 2 nos muestra una pared cuyo azimut es “A”, el azimut del Sol es “Z” y el ángulo d es el formado por los rayos del Sol con respecto a la normal de la pared.

De esta figura se deduce:

A = Z-d

El signo del ángulo d es el mismo del ángulo azimut Z del Sol, que es negativo tomado en sentido contrario a la marcha del reloj y positivo tomados en sentido de la marcha del reloj, siempre viendo al polo Sur.

La figura 3 nos muestra la misma pared pero con el instrumento de medición colocado sobre la misma, en donde el ángulo d es ahora el formado por la sombra del indicador, con longitud L de la sombra.

De la imagen se deduce:

Tang(d) = L/AG

 
 

Donde “L” es la longitud de la sombra, “AG” la altura del indicador, “A”, “Z” y “d” los ángulos ya identificados.

El azimut del Sol lo determinamos por las fórmulas de trigonometría esférica ya empleada en varias oportunidades en este Blog:

Sen (a) = Sen (l) x Sen (d) + Cos (l) x Cos (d) x Cos (H)

Cos (Z) = (Sen (l) x Sen (a) – Sen (d)) ÷ (Cos (l) x Cos (a))

Donde:

a = Altura del Sol sobre el horizonte en grados.

Z = Acimut del Sol en grados.

l = Latitud del lugar en grados.

d = Declinación del Sol en grados.

H = Ángulo horario al momento de la medición.

El ángulo horario H lo deducimos de la Hora Legal al momento de la medición:

H = HL + DL + ET

Donde:

H = Ángulo horario en grados (Hora Solar) al momento de la medición. (0º = 12:00 M)

HL = Hora Legal en grados al momento de la medición referida al UTC adoptado. Para Venezuela es el -4:30.

DL = Hora por diferencia por longitud geográfica expresada en grados. (Ver Trazado del Analema)

ET = Ecuación del Tiempo, en grados.

Las tablas con los valores de la declinación del Sol, de la Ecuación del Tiempo y la explicación del ángulo horario están expuestas en la entrada Trazado del Analema.

El instrumento una vez colocado en la pared debe estar alienado con la normal de la misma y esto se logra cuando el hilo de la plomada esté alineado con el indicador, para ello debemos rotar a uno u otro lado el instrumento hasta conseguir la coincidencia.

El prototipo de instrumento lo fabricaremos como todas las maquetas solares realizadas de cartón de construcción de 2 mm de espesor.

La imagen siguiente muestra la plantilla de la carátula graduada en milímetros, la misma tiene como dimensiones 200 x 200 mm.

Como he venido haciendo, me aprovecho de la tecnología para realizar la carátula utilizando un programa de diseño asistido por computador y a la exactitud de impresión de las impresoras láser. Para aquellos que no tengan acceso para realizar la carátula, puede intentar medir directamente la longitud de la sombra con una regla de precisión directamente sobre el instrumento.

La separación de 2 mm entre las líneas centrales es para compensar el grosor del cartón de construcción.

La figura muestra las medidas para el indicador del instrumento.

Las fotografías siguientes muestran el aspecto final del prototipo y su empleo.

Carátula graduada pegada al cartón.

Indicador y carátula recortados.

Para garantizar la perpendicularidad del indicador con la carátula graduada, se emplea un par de escuadras durante el pegado de los dos elementos.

Detalle del hilo de la plomada en el canto libre del indicador.

Instrumento colocado en la pared.

Nótese que el hilo de la plomada está alineado con el canto del indicador del instrumento.

Como el aparato diseñado es de cartón, es recomendable emplear las dos manos para sujetar firmemente el cuadrante graduado contra la pared, el calor del Sol tiende a curvar la carátula lo que nos introduciría mayores errores de medición.

Longitud de la sombra a las 7:15 AM hora local de 34 mm

Para el caso de la pared a la que le estamos determinando el azimut, realicé 4 mediciones en diferentes horas con el fin de determinar el valor medio entre ellas. Es de esperarse que los resultados obtenidos del azimut de la pared no sean idénticos y fácil de entender las causas entre las cuales están: la graduación de la carátula en milímetros, corte del borde del indicador quedando este con pequeños errores de paralelismo, la hora local en minutos, línea de la sombra sobre el cuadrante un poco difusa por la penumbra entre otras. No obstante el valor obtenido es bastante estable y consistentes, consiguiéndose una dispersión de los valores de azimut para la pared comprendido entre ±0,03º; dispersión que considero pequeña tomando en cuenta que la actividad es muy artesanal y sin instrumentos de medición precisos.

Para el día de la medición, 15-01-2.011,  la declinación del Sol era de -21,09º; la latitud del lugar +8,27º

Los valores de las mediciones que obtuve son los siguientes:

Hora local	L sombra (mm)	Azimut Sol	Ángulo d	Azimut pared
7:15 AM	34	64,99º	34,22º	30,77º
7:56 AM	30	61,74º	30,94º	30,80º
8:50 AM	23	55,53º	24,7º	30,82º
9:34 AM	16	47,98º	17,22º	30,76º

Azimut de la pared: 30,79º (valor promedio).

El azimut de la pared como lo estoy colocando está referido al plano meridional y mirando al Polo Sur, de acuerdo a la figura 3 este ángulo es contado en sentido anti horario, de manera que la pared  está girada hacia el Este en 30,79º. No importa como expresemos el azimut, en el sistema Náutico tiene el valor de 149,21º y en el sistema Astronómico toma el valor de 329,21º. La diferencia aparente entre los grados del azimut se debe solamente la referencia, que en el náutico se mide desde el polo Norte con sentido de giro de las agujas del reloj y el astronómico desde el polo Sur con el mismo sentido horario. Es gusto del que lo determina ya que a la final lo que necesita saber es la inclinación de la pared vertical con respecto al plano meridional y con este ángulo puede calcular el reloj de Sol Vertical Declinante.

La declinación del Sol para el día de las mediciones así como pasar la Hora Legal a Hora Solar Local no las saqué de las tablas que he venido utilizando en el Blog, sino que aproveché las bondades de una hoja de cálculos (la altura y azimut del Sol si los calculé con las fórmulas indiadas arriba) de difusión gratuita en la Internet. Esta interesantísima hoja de cálculos que nos permite determinar los valores de azimut del Sol, altura y demás datos astronómicos de interés para los constructores de relojes de Sol se puede bajar desde la página The Sundial Primer en el link SUN v.5.6. El autor es Ricardo Cernic, de Brasil. La hoja es muy fácil de utilizar.

Con el dato obtenido del azimut de la pared ya podemos calcular el reloj de Sol de Cuadrante Vertical Declinante. Para verificar el resultado obtenido de azimut, se hizo una pequeña maqueta de reloj de Sol Vertical que se muestra a continuación.

Maqueta realizada de acuerdo al azimut de la pared se muestra en la fotografía siguiente.

Obsérvese que el nomon del reloj posee la inclinación correspondiente al azimut de la pared.

La foto siguiente nos da la hora local Solar: 9:00 AM

Para el momento de la hora Solar, la hora Legal era de 8:54 AM. El desfase entre ellas (+6 minutos) es el esperado por la corrección geográfica del meridiano local y de la ecuación del tiempo.

En una entrega futura se desarrollará un reloj de Cuadrante Declinante para la pared tomando como referencia la maqueta; también se hará un repaso del cálculo requerido para su diseño ya que en esta oportunidad se determino la existencia de un error en las fórmulas expuestas en la entrada sobre los relojes de Sol de cuadrante Declinante.