PARADOJA MECÁNICA DE LEYBOURN.

PARADOJA MECÁNICA DE LEYBOURN.

TALLER E INVESTIGACIÓN.

Un enigma mecánico reproducido en casa.

Existe en el mercado un pequeño dispositivo educativo cuyo comportamiento a priori nos plantea lo que sería una paradoja mecánica .

Entendemos por paradoja un resultado contradictorio desde la lógica y al sentido común a partir de un conjunto de premisas y experiencias consideradas como válidas.

La vivencia diaria denuncia que todos lo cuerpos que son atraídos por la gravedad se desplazan desde el punto de mayor energía hacia el de menor energía si tienen el grado de libertad que les permita el movimiento. Sabemos que los cuerpos suspendidos al dejarlos libres caen y los que están sobre una rampa también “caen” descendiendo por la misma; siempre de un nivel de mayor energía potencial a uno menor.

Este dispositivo que parece retar las leyes de la naturaleza venciendo a la gravedad está conformado por un sólido de revolución en forma de bicono (dos conos unidos por sus bases) y de un par de rampas o rieles sobre los cuales el bicono se desplaza. La imagen siguiente nos muestra la disposición de este mecanismo.

Al colocar el bicono cerca del vértice que forman las rampas y soltarlo, el mismo se desplazará hacia la apertura de los rieles remontando la pendiente de la rampa. Si realizamos la experiencia modificando el ángulo que forman las rampas entre sí podemos constatar que mientras más grande sea este ángulo, el bicono “sube” la rampa con más velocidad y mientras más pequeño es el ángulo, la velocidad del bicono es menor llegando incluso a invertirse el sentido del desplazamiento, de manera que el bicono desciende por la rampa.

Fue el agrimensor ingles William Leybourn (1.626–1.716) quién describe el dispositivo por primera vez en un libro que publicó en el año de 1.694 con la intención de "apartar a la juventud de los vicios propios a los que es inclinada", lo que demuestra que esta preocupación no es nada actual y siempre a acompañado al hombre en todas las épocas.

Podemos construir este artefacto para recrear esta paradoja mecánica empleando elementos caseros como un par de vasitos cónicos de papel o de plástico para armar el bicono y cartón de construcción de 2 mm de espesor para hacer las rampas.

El éxito de esta recreación va a depender del cuidado que se ponga durante su fabricación.

La foto siguiente nos muestra un par de vasitos cónicos de papel antes de unirlos y un par unido con un pegamento por la base de los conos.

Hay que tener la precaución de emplear conos (vasitos) en el mejor estado posible, sin dobleces o abolladuras en sus generatrices y deben quedar lo más “redondo” y balanceado posible una vez unidos por sus bases.

La imagen siguiente muestra la plantilla para la fabricación de las rampas y sus soportes.

El ángulo de inclinación de las rampas está basado en el ángulo del cono de 39°.

La foto nos muestra las rampas o rieles de cartón listos para utilizar junto al bicono.

Armado el dispositivo podemos realizar la experiencia y analizar el comportamiento intrigante de este “juguete” científico. El video muestra el “enigma mecánico”.

En la fotografía siguiente podemos visualizar lo que está ocurriendo.

La foto es un montaje de la posición ocupada por el bicono en la parte más baja de la rampa y en el otro extremo que se corresponde con la parte más elevada. Si se traza una línea horizontal partiendo de cualquier punto del bicono de la izquierda, por ejemplo del borde superior como lo muestra la fotografía, notaremos que esta línea está por encima del mismo punto del bicono de la derecha. Lo que se está viendo en realidad es que el bicono “cae” por los rieles en vez de “subir”, pasando de un nivel de mayor energía potencial a uno menor energía, de manera que lo que percibimos no es más que una ilusión inducida por la pendiente de las rampas.

Esta fotografía destruye la paradoja mecánica y explica lo que ocurre.

Podemos hacer un pequeño análisis de las fuerzas que se presentan en el punto de contacto del bicono contra su riel y de aquí deducir alguna relación interesante que nos ayude a entender y predecir el comportamiento del bicono en función de su geometría y la de geometría de las rampas.

El peso del bicono en el punto de contacto en una de las rampas toma el valor de “P/2” y se descompone en su reacción “R” que es la normal a la rampa y la componente “A” perpendicular a “R”. El ángulo formado por “R” y “P/2” toma el valor del semi-ángulo “b” del cono como lo muestra la figura.

Del arreglo vectorial se deduce:

A = R x Tan (b)

La fuerza “A” es normal a la rampa y esta fuerza a su vez posee una componente “r” sobre la rampa. La figura siguiente nos da una vista de planta del dispositivo.

El ángulo “a” es el ángulo de apertura de los dos rieles medidos desde la mediatriz, haciendo centro de giro en la parte más baja de las rampas.

De aquí se deduce:

r = A x Tan (a)

El vector “r” es la fuerza que tiende a mover al bicono “cuesta arriba” sobre las rampas.

Sustituyendo “A” en esta última ecuación:

r = R x Tan (b) x Tan (a)

Por otro lado, el peso del bicono se descompone adicionalmente en la componente “b”, que es la fuerza que tiende a desplazar al bicono en “descenso” sobre la rampa. La figura muestra la disposición vectorial.

El ángulo “g

b = R x Tan (g)

Para que el bicono pueda “remontar” la pendiente de los rieles se debe cumplir la desigualdad:

r > b

Sustituyendo ……

R x Tan (b) x Tan (a) > R x Tan (g)

Eliminando “R”:

Tan (b) x Tan (a) > Tan (g)

Esta fórmula nos relaciona los tres ángulos presentes en el dispositivo, los cuales son:

a = semi-ángulo de apertura de los rieles.

b = semi-ángulo del cono.

g = ángulo de pendiente de las rampas.

De la expresión anterior podemos establecer lo siguiente:

Tan (b) x Tan (a) > Tan (g)

Si se cumple esta desigualdad, el bicono “sube” por las rampas.

Tan (b) x Tan (a) = Tan (g)

Si se cumple la igualdad, el bicono no se desplaza ya que está en equilibrio estático.

Tan (b) x Tan (a) < Tan (g)

Si se cumple esta otra desigualdad, el bicono “baja” por la rampa.

Ya disponemos de la relación matemática que nos permitirá diseñar nuestra paradoja mecánica en función de los ángulos asociados y predecir con bastante exactitud bajo que condiciones el bicono “sube”, “baja” o no se desplaza.

Para el caso del ingenio realizado en el blog los ángulos establecidos fueron:

a = 25°.

b = 19,5°

g < 9,4° (resultado de la desigualdad.).

El valor del ángulo g utilizado para el dispositivo fabricado fue de 7°.

Desde el punto de vista geométrico también podemos realizar un análisis similar.

La figura siguiente representa el desplazamiento del bicono sobre los rieles.

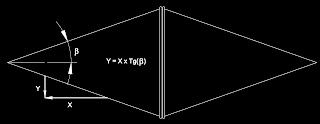
El vector “L” representa el recorrido del bicono sobre la rampa. En la medida que el sólido se desplaza sobre los rieles y como los mismos forman un ángulo entre ellos, el punto de contacto del bicono-rampa cambia de posición, este cambio está representado por el vector “X”. De la figura se deduce que el recorrido “X” puede determinarse por:

X = Z x Tan (a)

Por otro lado, en la medida que el punto de contacto sufre el desplazamiento “X” el bicono manifiesta un desplazamiento vertical “Y”, que se corresponde con un descenso del centro de gravedad del sólido. Ver figura siguiente.

Del dibujo se puede deducir:

Y = X x Tan (b)

Sustituyendo:

Y = Z x Tan (a) x Tan (b)

La imagen siguiente nos muestra la vista lateral del dispositivo.

De la figura se determina que el recorrido vertical de subida que realiza el punto de contacto del bicono al riel se determina por medio de:

H = Z x Tan (g)

Para que el bicono se desplace “cuesta arriba” la caída “Y” tiene que ser mayor que la subida “H”:

Y > H

De aquí:

Tan (b) x Tan (a) > Tan (g)

Este resultado es idéntico al obtenido anteriormente.

Cuando se cumple la desigualdad el bicono en realidad no “SUBE” la rampa como aparenta hacerlo sino que nuestro sentido de la vista es engañado por el efecto visual de las rampas, no percatándonos de que el bicono está cayendo en la medida que se desplaza por la pendiente. Ahora que sabemos el secreto, si observamos bien el bicono durante su desplazamiento cuesta arriba, notaremos que no sube la rampa.

Con la evidencia mostrada y los resultados de los análisis realizados, podemos concluir que la paradoja mecánica como tal es eso, una aparente contradicción con la experiencia y el sentido común.



ES HORA DE QUE EMPECEMOS A CAMBIAR……

ES HORA DE QUE EMPECEMOS A CAMBIAR……

José Cañizales Márquez en su libro “Así somos los Venezolanos”, toca un tema que lógicamente y según él debería disminuir con el transcurso del tiempo en la medida que la población de profesionales fuera aumentando, sin embargo pareciera que en los nuevos tiempos ha ganado vigencia este comportamiento tan vergonzoso.

Cañizales trata de conseguirle una explicación psicológica al fenómeno y en el capítulo denominado “El rastacuerismo del Venezolano” expone las posibles causas de este complejo que sienten muchos compatriotas ante la presencia de un profesional o un trabajador extranjero, particularmente si viene del Norte o de la Europa.

Este complejo de inferioridad como lo plantea el periodista José Cañizales, lo he podido presenciar muy de cerca durante mi vida profesional antes y ahora. En una de mis primeras entradas publicadas en el Blog con título “¿Somos los Venezolanos capaces de hacer las cosas bien?” denuncié en parte a este penoso comportamiento, que pareciera no quiere abandonarnos.

Sin embargo, este comportamiento que denuncio en esta entrada que pareciera que solamente toca los profesionales se extiende en realidad a toda la población en general y podemos ser testigos del mismo observando la conducta que asumen muchas personas cuando están en presencia de una persona que representa el “poder”, que acá en Venezuela normalmente se limita a los políticos y algún que otro personaje influyente.

Si bien esta actitud en parte tiene su origen en un complejo de inferioridad creo también que otra causa que lo desencadena es la inseguridad que posee la mayoría de nuestros profesionales por los conocimientos adquiridos, inseguridad producto de una educación conjugada con una formación deficiente por profundas fallas en nuestro sistema educativo que ha creado un contingente de profesionales incapaces de defender ni defenderse frente a un “experto”. Esta inseguridad paraliza al profesional precisamente por que no cree en sus conocimientos, ni en sus capacidades ni habilidades.

Personalmente he visto como profesionales que se desenvuelven con autoridad e imposición ante sus colegas se transforman violentamente en unos simples muchachos de mandado frente un “experto” extranjero, aceptando sin la menor reserva y crítica sus comentarios o ideas, obviando y/o silenciando a cualquiera que intente exigir explicaciones. Este comportamiento no sería preocupante si se tratara de hechos aislados, pero lamentablemente parece estar generalizado dentro de nuestra población de profesionales.

Aunque la intención de esta entrada no es la de crear un rechazo a las personas de otras nacionalidades, ni el rechazo irracional a los expertos requeridos por la nación, sí es un llamado a mis coterráneos para que se auto-analicen cuando estos sentimientos negativos afloren, rompiendo ese freno mental que tanto daño nos ha hecho y tratar de tomar una actitud crítica y profesional frente al “experto”, discutir o rebatir lo que dice con respeto y dominio de la causa.

Todos los venezolanos de alguna manera somos responsables y tenemos que minimizar y tratar de eliminar esta aborrecible actitud. Evidentemente la responsabilidad principal recae sobre las personas que llevan las riendas del País y de todos los gerentes o directores empresariales que por medio de la modelación den el ejemplo confiando más en sus intelectuales, técnicos y profesionales. Este sería el primer paso para minar este comportamiento que actualmente no tiene ningún basamento.

Paralelamente al cambio de actitud de los líderes políticos y empresariales se tiene que reforzar la educación (escolaridad) y la formación profesional, hay que promover políticas educativas en donde se valoren a nuestras mentes, a nuestros científicos, a nuestros artistas, nuestros técnicos, etc. un sistema que no nos denigre de manera velada o directa, que permita el desarrollo intelectual y emocional de los niños y jóvenes, que se nos enseñe a pensar y como dice el Dr. Luis Alberto Machado, que se nos enseñe ha ser más INTELIGENTES, cosa que ya se ha intentado en el pasado.

Tenemos que darnos la oportunidad para demostrarnos a nosotros mismos nuestras capacidades que nada tienen que envidiarle al resto del mundo y de esta manera empezar a salir de este desesperante subdesarrollo en que estamos hundidos, salir de la pobreza espiritual y de la marginalidad mental que cada día aparenta ganar terreno.

Las personas que tienen esa responsabilidad para con el País tienen que buscar los métodos y procedimientos en conjunto con nuestros grandes pensadores y escuchando a todo aquel que de alguna manera quiere cambiar de actitud frente a “la viveza criolla” que es una cara del oportunismo, que quiera cambiar de actitud frente al conocimiento, a los estudios y al trabajo para darle forma a un plan nacional de desarrollo personal, individual y colectivo en aras de buscar más independencia, bienestar y la tan cacareada soberanía.…. No podemos ser soberanos si somos una Nación dependiente de las otras, una Nación que no produce lo suficiente para mantener alimentada su población no puede ser soberana, una Nación que no cree, ni cuida, ni cultiva a sus intelectuales, profesionales y trabajadores no puede ser soberana. No pude ser soberana una Nación que no desarrolla tecnología. La soberanía está muy ligada al desarrollo tecnológico, no a la compra de tecnologías.

La tarea no es nada fácil, por que hay que luchar contra una cultura, una idiosincrasia, un modo de vida que es el ancla que nos impide el desarrollo como individuos, como colectivo y como Nación que aspira colocarse en el mundo, tenemos que luchar contra esos obscuros sentimientos de envidia y resentimiento para con nuestros compatriotas que de alguna manera sobresalen y que muestran habilidades y actitudes que son el motor para el desarrollo, Venezuela está llena de genios en todas las ramas de saber que han sido silenciados, maltratados, ignorados y hasta literalmente desterrados por este comportamiento absurdo de rechazo hacia el individuo que intenta sobresalir de la mediocridad, personas que a la final han fortalecido LA SOBERANÍA DE OTRAS NACIONES y no LA NUESTRA con sus trabajos y pensamientos……

… Se dice que el futuro está en los niños, pero, ¿quién los educará?, ¿quién les dará formación?, ¿las mismas personas que no creen en sí ni en sus compatriotas?... La tarea no es fácil por que no existe una receta ni una varita mágica que nos saque del atolladero, la única salida está en comprometernos con nosotros mismos y cambiar de actitud para comenzar, confiar en tus habilidades y conocimientos, en los de él y en los míos, si cambiamos como individuos cambiamos como colectivo.

A pesar de lo difícil que parece la tarea, creo que es posible el cambio, un cambio de actitud en las personas, en aquellas que domina su arte u oficio, que han desarrollado y fortalecido sus conocimientos de manera consistente y consciente para que se mantenga en su posición independientemente de quién tenga al frente. Todos los que de alguna manera logramos sobreponernos a estos sentimientos hemos logrado dar un paso adelante como personas, como trabajadores y como profesionales, aportando un granito de arena y marcando un precedente a favor de nuestra integridad y soberanía.

En lo personal, sólo se justifica la presencia de los “expertos” importados en aquellos campos que escapan de nuestra capacidad por tratarse de temas de vanguardia o poco convencionales e incluso en algunos convencionales que están en desorden y fuera de control con la idea de que aporten las soluciones que de momento no podemos ver, la presencia del experto es la oportunidad perfecta para que nos desarrollemos un poco más adquiriendo las competencias y “robándole” el conocimiento, haciéndolo nuestro, de manera que se pueda justificar y aprovechar la figura de este experto sin necesidad de sentirnos inferiores.

Es hora de que empecemos a cambiar……

CÁLCULO DEL PAR DE APRIETE O TORQUE DE UN TORNILLO.

CÁLCULO DEL PAR DE APRIETE O TORQUE DE UN TORNILLO.

Fórmulas para el torque. Material de los tornillos a varias temperaturas. Coeficientes de roce.

Eventualmente se nos presenta el caso de tener que “torquear” un tornillo en particular que no está dentro de las tablas de torques convencionales disponibles, bien sea por el diámetro del tornillo o por el material del mismo. En estos casos no nos que da más remedio que realizar nuestros propios cálculos para determinar el valor del par de ajuste o “torque teórico” requerido por nuestro nuevo caso.

Esta situación se me presento en muchas oportunidades trabajando en un taller mecánico de reparación de cilindros hidráulicos para la industria siderúrgica en donde se necesitaba en muchas oportunidades determinar los valores de ajuste para tornillos de hasta 95 mm de diámetro o determinar los valores de apriete para temperaturas por encima de los 100° C. Por otro lado debido a la gran variedad de tornillos empleados durante las reparaciones de más de 4.000 cilindros hidráulicos según las estadísticas del taller fue necesario realizar una serie de tablas con valores teóricos que coincidieran con las tablas de torques disponibles en el taller, las cuales no cubrían a los tornillos por encima de 42 mm de diámetro. De esta experiencia quedé claro que el cálculo del torque de un tornillo no es tan simple como aparenta.

Si bien es cierto que el método más popular para el ajuste de tornillos y tuercas es por medio del control del par de apriete o torque debido a su sencillez y economía, también es uno de los métodos más inciertos en cuanto a la garantía de la fuerza de unión en un ensamble apernado.

El control del par de apriete se consigue normalmente ajustando un torquímetro a un valor especificado bien sea por el fabricante del equipo o por los valores indicados en las tablas de torques. Recordemos que el torquímetro no mide la tensión o precarga en el tornillo sino el valor del par aplicado. Valor este que es prácticamente producto de la fricción entre los flancos de las roscas tornillo-tuerca y del roce entre la cabeza del tornillo y su arandela, solamente el 10% del torque total de ajuste aplicado corresponde a la generación de la fuerza de precarga. El problema de este método se presenta cuando es utilizado indiscriminadamente sin tomar en cuenta la aplicación de la unión apernada.

En la literatura técnica podemos encontrar una fórmula empírica muy simple que nos relaciona el par de ajuste con la fuerza de precarga generada por el tornillo en función del diámetro del mismo y de una constante de proporcionalidad adimensional.

Esta sencilla ecuación válida en la zona elástica del material del tornillo es:

MA = K x d x FM …. [1]

En donde “MA” es el par o torque aplicado al tornillo (N.m, lbs.in), “d” es el diámetro nominal del tornillo (mm, pulg), “FM” es la precarga del tornillo (N, lbs) y “K” la constante de proporcionalidad que normalmente se determina experimentalmente.

Este factor “K” se le denomina con frecuencia como “factor de tuerca” con un valor muy bajo parecido al del coeficiente de fricción, sin embargo no debe confundirse el factor “K” con el coeficiente de fricción estático del material.

La tabla siguiente muestra los valores típicos del factor “K” para tornillos de acero.

La ecuación anterior puede emplearse siempre y cuando el valor de “K” esté correctamente determinado por el usuario. Sin embargo la experiencia a demostrado que asumir un valor de “K” es arriesgado de acuerdo a la aplicación del tornillo y no debe sobre-estimarse la importancia del torque de apriete en aquellos elementos críticos de gran responsabilidad.

De la fórmula MA = K x d x FM, el valor de la precarga “FM” del tornillo se determina a partir del valor de tensión a la tracción admisible sobre el material del tornillo que en la mayoría de los casos se basan en el 90% del valor del punto de fluencia proporcional “Rp” o límite elástico inferior “ReL” para los tornillos métricos y entre el 70% y 90% de la tensión de prueba para los tornillos imperiales.

Por ejemplo, un tornillo de calidad 5.6 posee un valor Rp = 30 N/mm2 (nominal) con lo que el cálculo de la fuerza de precarga se realiza con el 90% de este valor, es decir con 27 N/mm2 de tensión.

La fórmula para determinar la fuerza de precarga para el caso del 90% del límite de fluencia (Rp o ReL) del material del tornillo es:

FM = 0,9 x Rp x As …. [2]

Para efectos del cálculo de la fuerza, el área que se emplea para determinar el valor de la tensión es la sección resistente nominal de la rosca, la cual se calcula por:

…. [3]

Donde:

As = área o sección resistente efectiva.

d2 = diámetro primitivo de la rosca. (ISO 724)

d3 = diámetro de núcleo de la rosca.

Los valores de d2 y d3 se consiguen en las tablas de las roscas.

Como d2 y d3 dependen del paso y del perfil de la rosca, la sección resistente para los tornillos métricos se puede determinar por:

…. [4]

Donde “d” es el diámetro nominal de la rosca del tornillo y “P” el paso de la rosca.

La norma VDI 2230 expone un grupo de fórmulas más extensas y complejas en donde se relacionan la geometría del tornillo y del agujero, el material, los coeficientes de fricción rosca-rosca y cabeza-asiento permitiéndonos calcular los valores de torque para cualquier tipo de tornillo.

Estas formulas parten del principio que el par de ajuste o torque aplicado total para crear la precarga del tornillo es producto de la suma de los pares parciales creados por la fricción tanto de la rosca como de la cabeza del tornillo.

MA = MG + MK …. [5]

“MG” es el par o torque generado por la rosca y “MK” el momento producido por la fricción por la cabeza o la tuerca del tornillo producto de la fuerza de precarga “FM”.

El momento de ajuste que se origina por la precarga sobre la rosca se puede determinar, prescindiendo del desarrollo analítico, por medio de la fórmula:

…. [6]

Donde:

MG = Momento o par aplicado en la rosca.

FM = Fuerza de precarga sobre la rosca.

d2 = diámetro primitivo de la rosca.

P = Paso de la rosca.

uG = Coeficiente de roce rosca-rosca.

El número 1,155 es la secante del semi-ángulo del flanco de la rosca. Para la tortillería métrica el ángulo del flanco de la rosca es de 60°. De aquí que; Sec (60/2) = 1,155 redondeando.

El par creado por el roce en la cabeza del tornillo se determina por:

…. [7]

Donde:

MKR = Momento o par aplicado en la cabeza del tornillo o en la tuerca.

FM = Fuerza de precarga sobre la cabeza o tuerca.

DKM = Diámetro medio de fricción del área anular de deslizamiento de la cabeza o de la tuerca.

uK = Coeficiente de roce de la cabeza o tuerca contra el asiento.

El diámetro medio de deslizamiento “DKM” se determina por:

…. [8]

En donde “dW” es el diámetro de asentamiento de la cabeza o de la tuerca que aparece en las normas sobre los tornillos y es aproximado al hexágono de la tuerca o cabeza del tornillo (dW = s) o el diámetro de la cabeza para los tornillos allen y “dh” es el diámetro del agujero donde asienta la cabeza o la tuerca, normalmente grado medio según DIN 69.

Sumando ambas expresiones nos queda que el torque de ajuste se determina por:

…. [9]

Las letras que se emplean en las formulas se corresponden a las indicadas en la norma VDI 2230.

Esta última fórmula nos permite determinar el par de apriete aplicado al tornillo o a la tuerca para conseguir el valor de la fuerza de precarga en función de los parámetros físicos y mecánicos del tornillo como la rosca, el agujero de asentamiento de la tuerca o la de la cabeza, del coeficiente roce entre los materiales de fabricación de la unión apernada y del paso de la rosca.

Es interesante observar que la expresión encerrada en el paréntesis de la fórmula [9] al ser dividida por el diámetro nominal “d” de la rosca se obtiene el valor del factor de tuerca “K” empleado en la fórmula [1]:

…. [10]

La fuerza máxima de precarga sobre el núcleo del tornillo dentro de la zona elástica del material se consigue cuando las tensiones originadas por la precarga alcanzan el valor del punto de fluencia del material o el punto de proporcionalidad Rp0.2. Esta tensión final o reducida está definida por la presencia simultánea de tensiones de tracción producto de la precarga y de tensiones de corte por torsión causadas por el par de apriete.

De acuerdo a las teorías sobre la resistencia de los materiales cuando una barra está sometida a esfuerzos combinados, la tensión resultante se calcula por:

…. [11]

Sin tomar en cuenta la demostración analítica, de la fórmula [11] se deduce que la fuerza de precarga “FM”, se calcular por:

…. [12]

La sección resistente “AS” o el área efectiva del tornillo sometido a los esfuerzos y se determina por medio de la fórmula [3] la cual puede escribirse:

…. [13]

y “dS” se determina por:

…. [14]

El número contante de 0,9 es el indicador del 90% del punto de fluencia, este valor puede ser sustituido de acuerdo a la aplicación del tornillo por otro valor.

Con las fórmulas [9] y [12] ya estamos en capacidad de calcular la fuerza de precarga y el par de ajuste aplicado para cualquier unión apernada o elaborar nuestras tablas de torque según nuestras necesidades.

Para aclara un poco más el uso de las fórmulas [9] y [12] calcularemos la precarga y el torque o par de ajuste necesario para un tornillo hexagonal DIN/EN/ISO 4014; M 30 rosca gruesa calidad 8.8, laminado, pavonado y montado en seco sin lubricación a 20ºC.

Parámetros del tornillo M 30:

Paso = 3,5 (Según norma)

d2 = 27,727 (Según norma)

d3 = 25,706 (Según norma)

dW = 42,75 (Según norma)

Rp02 = 660 N/mm2. (Calidad 8.8 y d<16 a 20° C, Norma ISO 898. Ver tabla al final)

uG=uK = 0,12 (Ver tablas al final del artículo)

dS = 26,7165 Cálculo por [14]

AS = 560,595 Cálculo por [3]

dh= 33 (Por norma DIN 273 grado medio – Agujero)

DKM = 37,875 Cálculo por [8]

Resolviendo la fórmula [12] obtenemos el valor de precarga:

FM = 300 kN

Con el valor de la precarga calculamos el par de ajuste requerido por medio de la ecuación [9]:

MA = 1.425 Nm

Otro ejemplo:

Tornillo hexagonal M8 rosca gruesa calidad 12.9 según DIN/EN/ISO 4014, lubricado con aceite durante el montaje.

Paso = 1,25 (Según norma)

d2 = 7,188 (Según norma)

d3 = 6,466 (Según norma)

dW = 11,63 (Según norma)

Rp02 = 1.100 N/mm2. (Calidad 12.9 a 20° C, Norma ISO 898. Ver tabla al final)

uG=uK = 0,1 (Ver tablas al final del artículo)

dS = 6,827 Cálculo por [14]

AS = 36,61 Cálculo por [3]

dh= 9 (Por norma DIN 273 grado medio – Agujero)

DKM = 10,315 Cálculo por [8]

Resolviendo la fórmula [12] obtenemos el valor de precarga:

FM = 32,8 kN

Con el valor de la precarga calculamos el par de ajuste requerido por medio de la ecuación [9]:

MA = 37,1 Nm

Podemos comparar estos valores con los indicados por la tabla de la VDI expuesta en la entrada ¿Cómo manejar las tablas de torques?, los valores son muy próximos.

Si efectuamos los mismos pasos para un tonillo hexagonal M8 rosca fina y calidad 12.9 obtendremos los valores siguientes:

FM = 35,6 kN

y

MA = 39,2 Nm

Podemos confirmar que los tornillos rosca fina son capaces de generar mayores precargas y admiten mayor par de ajuste que los rosca gruesa o normal, quedando en evidencia la razón principal por la cual las tablas de torques no son “extrapolables” a los diferentes tipos de roscas o de normas de fabricación de los tornillos. Para cada caso existen las respectivas tablas.

Debo advertir que estos resultados se consideran válidos solamente para tornillos nuevos y que cumplan con los parámetros indicados por las normas pues en caso contrario se pueden “sobre torquear” a los tornillos. Se insiste en tornillos nuevos ya que se ha comprobado que el coeficiente de roce varía fuertemente al ser ajustado y aflojado en varias oportunidades un tornillo, observándose variaciones del coeficiente de roce en un factor de al menos 3. Esta es una de las razones por la cual se recomienda siempre no reutilizar la tornillería y la misma debe ser cambiada cada vez que se desmonte la unión, más aún, debido al uso del tornillo, a las imprecisiones durante el ajuste, a las fuerzas de trabajo y al hecho de que se utilizan al 90% del punto de fluencia, no es extraño que el mismo al ser desmontado ya esté “sentido”.

Es oportuno también recordar que este cálculo como lo mostré es valido para uniones metal-metal, sin juntas blandas de por medio en donde esto debe considerarse al igual que la aplicación. Por ejemplo, se dice que el par de ajuste de los tornillos para las torres eléctricas es aproximadamente la mitad del calculado con el único fin de evitar que la capa de recubrimiento galvánico de la estructura se agriete al ajustar los tornillos. En fin cada caso debe ser estudiado.

Como aclaratoria final, cuando se emplea un torquímetro el valor del torque aplicado en el tornillo va ha depender de la velocidad con que se realiza el ajuste, indicándonos prematuramente el instrumento que llegó al valor de ajuste cuando este se realiza rápidamente, de manera que los valores de torque más cercanos al indicado por el instrumento se obtiene efectuando un apriete lento y continuo. Se suele recomendar cuando son varios tornillos realizar el torqueado en CRUZ o “X” y comenzando con un porcentaje del valor final requerido, como por ejemplo ajustando primero a un 30% los tornillos, luego al 60% y por último al 100% del torque requerido. Con esto se obtiene una mejor garantía del ajuste final de la tornillería.

Las cuatro tablas siguientes nos muestran algunos datos necesarios de conocer a la hora de “torquear” un tornillo, como es la reducción de la capacidad de carga del material en función de la temperatura de trabajo, la resistencia del material y el roce.

Coeficientes de roce en la cabeza.

Coeficientes de roce en la rosca.

Material de los tornillos de acero.

Límite de fluencia en función de la temepratura.

Espero que esta entrada sea de utilidad a quienes están buscando información sobre el par de ajuste o torqueado de los tornillos en función de sus parámetros mecánicos y del material.

RELOJ DE SOL POR REFLEXIÓN O CATÓPTRICO.

RELOJ DE SOL POR REFLEXIÓN O CATÓPTRICO.

Reloj de Sol Catóptrico Ecuatorial.

Construyendo Relojes de Sol.

Así como el reloj de Sol de Difracción, el reloj Solar por reflexión sustituye la sombra indicadora de la hora del nomon por un rayo de luz. Esta particularidad nos permitiría agrupar a este par de relojes de Sol en un conjunto que bien podría denominarse “Relojes de Sol Invertidos”. La denominación de este tipo de relojes por reflexión se conoce desde la antigüedad como relojes Catóptricos ya que el arte o la ciencia que estudia la reflexión de la luz se denomina Catóptrica.

En esta entrada intentaremos elaborar un reloj “Catóptrico” de cuadrante Ecuatorial a partir de un espejo plano, el cual reflejará la luz del Sol a modo de “aguja luminosa” que pivotando en el centro del cuadrante al ritmo de la naturaleza nos indicará la hora verdadera.

Como primer proyecto y ensayo a la vez, este reloj de Reflexión está basado en los relojes de cuadrante Ecuatorial, por ser este tipo de relojes los más fáciles de hacer sin necesidad de recurrir a complejas fórmulas ni a las coordenadas celestiales y horizontales, pues, basta con tener claro lo concerniente a los cuadrantes Ecuatoriales en donde la divisiones de las horas se consiguen por simple división del cuadrante en ángulos iguales uniformemente repartidos alrededor del centro del mismo que es donde nace el nomon.

Para entender el principio de funcionamiento de este reloj de Reflexión Ecuatorial, recordemos que los relojes de Sol de Cuadrante Ecuatorial copian a la perfección el movimiento diurno del Sol en la esfera celeste independientemente de la estación del año en que nos encontremos. Se puede demostrar fácilmente con la geometría de bachillerato que para efecto del reloj de Sol de cuadrante Ecuatorial, el Sol “gira” alrededor del nomon en la medida que transcurre el día, de manera que la sombra del estilo o nomon realiza el recorrido angular de 15° por cada hora transcurrida. Esta demostración geométrica se la dejo al lector como un pequeño ejercicio mental.

En este diseño de reloj de Sol de Reflexión de cuadrante Ecuatorial, el estilo es sustituido por un estrecho espejo plano, de manera que la luz “rebotada” proyecta una franja de luz sobre el cuadrante solar que pareciera surgir del origen de las líneas horarias. Como el espejo posee su superficie reflectora mirando al cielo y paralela al eje del mundo, la luz reflejada reproduce de forma especular el movimiento que haría la sombra del estilo sobre el cuadrante.

Debido al diseño conceptual del reloj, el mismo contempla un cuadrante solar graduado por ambas caras y que puede ser colocado en una de las dos posiciones preestablecidas sobre el soporte en función de la época del año, el soporte del cuadrante es también el soporte del espejo plano y su forma garantiza el paralelismo del espejo con el eje de rotación de la Tierra y del cuadrante con el ecuador celeste. Sobre el espejo se colocará una máscara para dejar al descubierto una estrecha franja reflectora y de esta manera generar la aguja de luz que marcará la hora.

El reloj de Sol de Reflexión que estamos diseñando está ubicado dentro del Trópico de Cáncer, por tal motivo, el Sol en su deambular anual recorre la bóveda celeste en dirección Norte-Sur pasando por el cenit, de manera que en los meses de Enero, Febrero, Marzo, Septiembre, Octubre, Noviembre, Diciembre y parte de Abril, el Sol se encuentra al Sur iluminando la cara del cuadrante solar que mira a esa dirección, mientras que en los meses de Abril (parte), Mayo, Junio, Julio y Agosto el Sol es encuentra al Norte iluminando la otra cara del cuadrante solar. Esta es la razón del porqué se requiere que el cuadrante Ecuatorial esté graduado por ambas caras y porqué ocupa dos posiciones diferentes según esté el Sol al Norte o al Sur.

Las imágenes siguientes nos muestran al reloj de Sol con el cuadrante solar colocado para el período en que el Sol se encuentra al Norte y la posición para la época en que el Sol está al Sur respectivamente.

Para este pequeño proyecto se empleó un espejo sobrante del Calidoscopio mostrado en otra oportunidad; las dimensiones del espejo plano son 25 x 3 x 120 mm.

Debido a las pequeñas dimensiones del espejo, el reloj es de dimensiones modestas y el mismo está diseñado para hacerlo con cartón de construcción de 2 mm de espesor, material que he utilizado para la realización de todas las demás maquetas de los diferentes tipos de relojes de Sol mostrados en este Blog.

La imagen siguiente muestra los planos dimensionales de los diferentes componentes del reloj de Sol de Refracción.

Las figuras siguientes muestran las plantillas del reloj de Sol.

Los elementos identificados como “soporte reloj”, son los encargados de recibir al cuadrante Ecuatorial solar y fijarlo con la inclinación con respecto a la vertical igual a la latitud del lugar, los componentes denominados “soporte de espejo” van en las caras internas del soporte reloj entre las ranuras para el cuadrante, sobre estas piezas es que se fija el espejo que nos servirá de nomon luminoso. La profundidad de las ranuras para recibir al cuadrante Solar contempla el espesor del vidrio del espejo con el fin de que el centro del cuadrante coincida con la cara platinada. Sobre el espejo se colocará la “mascara” para permitir solamente la reflexión de un estrecho haz de luz, que se proyectará sobre el cuadrante Ecuatorial. El espesor de la mascara debe ser lo menor posible y en mi caso empleé únicamente papel bond.

Mejor que las palabras, la serie de fotografías siguientes nos muestran paso a paso el proceso de fabricación y armado del reloj de Sol por reflexión.

Plantillas del reloj pegadas al cartón de construcción.

Piezas recortadas y listas para ensamblar.

Espejo.

Armado del soporte reloj y colocando soporte del espejo.

Soporte con el espejo colocado.

El espejo con la máscara de papel.

Vista lateral de reloj mostrando la inclinación del cuadrante Solar.

Hora solar, las 11:00 AM

Reloj de Reflexión Ecuatorial junto al reloj de Sol Ecuatorial.

El reloj diseñado acá está calculado para la Ciudad de Puerto Ordaz (Latitud norte de 8,27°), por lo que para otras latitudes el ángulo indicado en los planos de 8,27° debe ser sustituido por el del lugar donde se colocará este pequeño reloj de Sol por reflexión.

Durante el seguimiento de las horas indicadas por el reloj de Sol por reflexión, pude notar que el mismo no puede dar la hora por debajo de las 10:30 AM o por arriba de la 1:30 PM aproximadamente, ya que la “aguja” indicadora de luz deja de ser visible. Este defecto tiene su origen en el espejo utilizado y es un comportamiento no previsto durante el diseño (error de principiante) del reloj por estar centrado en la idea principal y obviando algunas consideraciones. No obstante, la práctica marca la pauta y nos da la oportunidad de mejorar las futuras construcciones al mismo tiempo que incentiva la búsqueda de la causa de los errores cometidos o de las deficiencias en los análisis realizados.

Al trazar la trayectoria de los rayos de luz reflejados, rápidamente caemos en cuenta de la causa de la falla. El espejo utilizado es de los normales de vidrio en donde el platinado está en la parte inferior, de manera que a partir de cierto ángulo de incidencia la luz rebotada es interceptada por la máscara que está en el vidrio sobre el espejado. La máscara se encuentra 3 mm por encima de la capa reflectora lo que limita fuertemente el ángulo horario barrido por la aguja luminosa como lo muestra la figura.

A pesar de este detalle perturbador, el reloj mostró su principio de funcionamiento basado en la reflexión de la luz Solar. El diseño puede ser mejorado notablemente si empleamos un espejo cuya capa platinada esté en la superficie superior (no lo pude conseguir) y no en la inferior como el espejo empleado.

Si bien en esta entrega intentamos el desarrollo de un reloj Catóptrico de cuadrante Ecuatorial por su simplicidad, su funcionamiento nos abre una pequeña brecha que nos permite entrever las posibilidades de diseño para este tipo de relojes Solares por reflexión, dejando en manos de los lectores el desarrollo creativo de los mismos.

INSERTANDO UN ARCHIVO MACROMEDIA FLASH (*.SWF) EN POWERPOINT.

INSERTANDO UN ARCHIVO MACROMEDIA FLASH (*.SWF) EN POWERPOINT.

Resolviendo el problema de insertar animaciones FLASH.

En más de una oportunidad he querido insertar dentro de una presentación de POWERPOINT un “video” realizado en FLASH con resultados negativos, teniendo que recurrir al “truco” de correr la animación FLASH y hacer una grabación de la pantalla.

Aunque este procedimiento es funcional también está muy limitado, ya que lo que se muestra en la presentación es la copia de la animación como tal sin opción de utilizar la animación con todo su potencial.

Aunque realicé varias búsquedas en Internet, los procedimientos mostrados no me funcionaron, tal vez por falta de claridad en algún paso o por mala interpretación del contenido de los artículos que dan las explicaciones de cómo hacerlo.

Este problema felizmente resuelto es el motivo para la creación de esta entrada con la intención de facilitarle aún más el procedimiento a aquellos que como yo no logramos el objetivo por alguna razón.

Mis presentaciones la he venido realizando en PowerPoint 2007 por la mayor flexibilidad que posee esta versión sobre la 2003, de manera que la explicación que doy es para la versión 2007, sin embargo, es aplicable también al PPT 2003 desde su entorno.

Para evitar el primer inconveniente hay que tener instalado el reproductor de FlashPlayer. Si tenemos dudas al respecto lo bajamos e instalamos desde la página WEB de Adobe.

Al abrir PowerPoint 2007, verificamos si está una pestaña en el cintillo de opciones con el nombre de “PROGRAMADOR” como lo muestra la imagen siguiente.

De no estar la pestaña, presionamos el botón grande (arriba a la izquierda) donde está el logotipo de OFFICE y en la ventana que se abre le damos “click” al botón de “Opciones de PowerPoint”, en la ventana emergente marcamos la casilla “Mostrar Ficha Programador en la cinta de Opciones” aceptamos y debe aparecer la pestaña de “PROGRAMADOR”.

Con el archivo PPT abierto le damos a la pestaña “PROGRAMADOR” y en ella, en el cuadro de “CONTROLES” le damos un “clic” al ícono que posee un martillo cruzado con una herramienta, se abrirá una ventana con una lista de controles y buscamos “Shockwave Flash Object”. La imagen nos muestra lo descrito.

Le damos al botón “Aceptar”, el cursor toma la forma de cruz y con ella trazamos un cuadro, el cual tendrá una “X” que lo atraviesa.

Con el cuadro marcado pulsamos al botón de “PROPIEDADES” y en la ventana que aparece en la casilla de “Playing” colocamos “True”, en la casilla de “EmbedMovie” cambiamos la opción de “False” a “True”.

En la casilla “Movie” colocamos la URL completa de la animación que queremos insertar. La dirección URL tiene que contener el nombre del archivo de la animación que queremos en la presentación. Recordemos que en la dirección URL el archivo de la animación debe tener por extensión “swf”

Hecho esto cerramos la ventana y le damos a “F5” para ver la presentación, debe aparecer la animación Flash con todos sus controles y botones activos. La animación sólo corre bajo el modo de presentación.

Puede darse el caso en que tengamos la URL de la animación y sin embargo en ella no se vea la extensión “swf” del archivo, si esto ocurre la animación FLASH no correrá en nuestra presentación. La manera como he resuelto esta situación es buscando la animación FLASH en la carpeta de temporales de internet y correrla desde allí para copiar la URL correcta.

Para localizar el archivo de la animación que nos interesa en la carpeta de “archivos temporales de Internet”, entramos en “Opciones de internet” desde el Panel de Control o desde las “Herramientas” del Explorador de Internet. En la ventana que se abre, en la pestaña de “General” le damos “clic” al botón de “Configuración” del “Historial de exploración”, le damos a “Ver archivos” y se abre una ventana en donde están todos los archivos abiertos y guardados en la carpeta “archivos temporales de Internet”, allí buscamos la animación que es posible que no tenga la extensión SWF, para localizarlo nos guiamos por el nombre que aparece en la URL donde está la animación y buscamos en la pestaña que dice “Tipo” el que tenga la descripción “Shockwave Flash Object”, allí se puede ver la dirección URL o le damos doble “click” al archivo para qué corra, debe abrirse una página WEB con el video o la animación solamente. Copiamos la URL y la insertamos en la presentación como ya se describió.

Otra opción para insertar una animación FLASH consiste en buscar el archivo de la animación que nos interesa montar en la presentación de PowerPoint y copiarlo en una carpeta del disco duro.

Efectuando los pasos anteriores para encontrar el archivo de la animación en la carpeta de “temporales de Internet”, buscamos el archivo con extensión “swf”, si no tiene la extensión “swf” como el caso ya comentado, no correrá la animación en la presentación, si tiene la extensión, lo copiamos en la carpeta que nos interese o en la misma donde estará el archivo PowerPoint.

Para insertar la animación copiada en el disco duro se realizan todos los pasos ya descritos desde la primera imagen, pero en la casilla “Movie” colocamos la ruta en donde está el archivo “SWF”, por ejemplo: C:\Presentacion\Detalles\calculos\animacion.swf. Cerramos el cuadro y pulsamos “F5” para ver la animación.

He probado una presentación PPT con la animación insertada en otros computadores en donde no está el archivo copiado tanto en PowerPoint 2007 como en el 2003 (modo compatibilidad) y la animación ha corrido perfectamente, indicándome que no es necesario arrastrar consigo el archivo SWF de la animación junto con la presentación en PowerPoint.

Tengo la esperanza que este pequeño post pueda cumplir su función con algún Internauta, que como en mi caso no haya logrado insertar una animación Flash en su presentación PPT.