CÁLCULO DE LA LONGITUD ROSCADA.
Aunque este tema está más expuesto el la red que el cálculo
del par deapriete de los tornillos y tuercas, no suele tomarse en cuenta
durante los cálculos del par de ajuste, ya que se “asume” que la longitud
roscada de enganche es la correcta y la misma no va a fallar bajo los esfuerzos
de apriete y de trabajo. Este punto es cierto siempre que se está trabajando
con elementos que cumplan con la norma en cuanto a los criterios de diseño de
las roscas y del material de las mismas,
aquí me refiero tanto a la rosca macho como a las roscas hembras o
tuercas.
Es buena práctica de diseño que la rosca hembra sea la más
resistente estructuralmente y se espera que el tornillo sea el que falle a
nivel de las roscas que no están bajo carga, que el núcleo del tornillo rompa
por los esfuerzos y en el peor de los casos que la rosca del tornillo se
“barra” y no la rosca hembra o tuerca. Eventualmente nos topamos con algún caso
que es la “excepción de la norma” en donde el material de fabricación de la
tuerca es mecánicamente inferior a la resistencia del tornillo. Es en estos
casos donde hay que poner especial atención si no queremos tener aflojamientos
y roturas espontáneas de la unión roscada.
Entendemos como longitud roscada de enganche a la longitud
de contacto entre la rosca del tornillo (rosca macho) y la rosca de la tuerca o
la rosca hembra. De la misma manera que para el cálculo del momento de apriete
de un tornillo, en la longitud de enganche de una unión roscada influye el
material de fabricación, las tolerancias de fabricación y el perfil de las
roscas o la norma a la cual pertenecen.
En esta entrada nos limitaremos a las roscas (tornillería)
métricas ISO basadas en la DIN 13 y las fórmulas expuestas acá son válidas sólo
para este tipo de flanco a 60º.
La longitud roscada de enganche se determina básicamente
por las tensiones al corte que sufre la rosca al ser sometida a las fuerzas de
apriete y trabajo. Evidentemente, que los cálculos expuestos no toman en cuenta
las deformaciones que sufre la rosca y que las fuerzas que actúan sobre el
tornillo son coaxiales al eje de la unión y uniformemente repartidas sobre los
flancos.
La figura siguiente permite aclarar la simbología y los
parámetros utilizados para el cálculo de la longitud de rosca.
FIGURA 1
De la figura:
d = Diámetro externo de la rosca macho o tornillo.
d2 = Diámetro primitivo de la rosca macho.
d3 = Diámetro interno de la rosca macho.
D = Diámetro (externo) de la rosca hembra o tuerca.
D2 = Diámetro primitivo de la rosca hembra.
D1 = Diámetro interno de la rosca hembra.
P = Paso.
60º = Ángulo del filete de la rosca.
H = Altura del triángulo base de la rosca.
Las roscas quedan definidas por el diámetro nominal “d”, el
cual no toma encuentra las tolerancias de fabricación. Por ejemplo, una rosca
M42x2 posee un diámetro nominal de 42 mm y paso de 2 mm por tratarse de una
rosca métrica “M”, dependiendo de la tolerancia este diámetro (al igual que
todos lo demás) tendrá una medida final diferente a 42. Si la tolerancia es 6g,
el diámetro estaría comprendido entre 41,96 mm y 41,68 mm. De la figura se
pueden deducir las relaciones existentes entre los diámetros, altura y el paso
de la rosca, relaciones mostradas en las tablas normalizadas de las roscas.
Desde el punto de fabricación los diámetros deben quedar
comprendidos dentro de las tolerancias de la rosca, que el caso más usual en
tornillería es la calidad media, es
decir 6g para la rosca macho y 6H para la rosca hembra. Al igual que el sistema
de tolerancias dimensionales, la letra define la posición de la zona de
tolerancia con respecto a la línea de referencia y el número el Intervalo de
Tolerancia (IT) que define la amplitud de la misma. En el sistema métrico, las
tablas de roscas que están bien definidas dan los valores máximos y mínimos de
todos los diámetros que poseen las roscas en función a la tolerancia; un buen
ejemplo de este tipo de tablas está expuesto en la norma DIN 13.
La figura 2 nos muestra el ensamble tornillo/tuerca, en el
dibujo sólo se dejaron los datos de interés para deducir la fórmula que
permitirá calcular la longitud roscada de enganche.
FIGURA 2
El plano crítico de corte de la rosca hembra queda definido
por el diámetro externo mínimo (según tolerancias) de la rosca macho, este
plano define el ancho “T” de la sección de corte del filete que estará sometida
al corte debido a las fuerzas resultante del apriete de las roscas más las
fuerzas de trabajo. “J” es el juego entre roscas producto de las tolerancias de
fabricación de la rosca macho y de la rosca hembra.
De acuerdo a la figura, la sección de corte de la rosca
hembra queda definida como:
Donde:
Ac = Área sección de corte.
dmin = Diámetro mínimo de la rosca
externa macho.
T = Ancho de la sección de corte en la rosca
hembra.
n = Número de espiras.
Si el número de espiras “n” se toma como 1, el área de corte calculada sería la sección
unitaria, es decir por espira. De la figura anterior es fácil entender porqué
se toma el diámetro menor de la rosca macho, ya que el ancho de la sección de
corte se hace menor.
Por otro lado se tiene que:
Donde:
n = Número de espiras.
L = Longitud de rosca.
P = Paso de la rosca.
De la figura 2 también se puede deducir que:
Para encontrar la relación existente entre el juego “J”
entre flancos de las roscas y las dimensiones del perfil triangular base nos
apoyaremos en la figura 3.
FIGURA 3
Haciendo coincidir los flancos de las roscas macho y hembra
se puede llegar a la siguiente expresión:
Desde el punto de vista del juego “J” se toma el diámetro
primitivo máximo de la rosca hembra (D2max), ya que el juego es mayor
cuando el diámetro primitivo de la rosca hembra toma su máximo valor.
La siguiente relación se deduce de la figura 1:
Combinando [3], [4] y [5] se tiene la ecuación matemática
que nos permite hallar el ancho de la sección sometida a corte “T” en función
del paso “P” de la rosca, del diámetro mínimo de la rosca macho y del diámetro
primitivo máximo de la rosca hembra.
Finalmente, sustituyendo [6] y [2] en la fórmula [1]
tenemos el área de corte de la rosca hembra, cuya expresión final es:
Esta última fórmula es idéntica a la empleada en la norma
ANSI para calcular la sección de corte de la rosca hembra. No es una simple
casualidad que la norma VDI y la ANSI coincidan en la ecuación ya que el perfil
de las roscas Imperiales Americanas “UN” es triangular con 60º de ángulo entre
flancos, es decir ambos perfiles cumplen con las mismas reglas en cuanto al
triángulo base del perfil. Evidentemente, en las roscas “UN” se emplean las
pulgadas y por el paso de la rosca el número de hilos sobre pulgadas.
Con la fórmula [7], la resistencia al corte del material de
fabricación de la rosca hembra y la fuerza aplicada sobre la misma, se puede
calcular la longitud roscada de enganche “L”.
Si hacemos “L=1” en la ecuación [7], se obtiene el área de
corte unitario “Ac1” de la rosca hembra.
En principio la rosca hembra debe ser más resistente que la
rosca macho o que el tornillo como tal. Como punto de partida se asume que la
capacidad de carga al corte de la rosca hembra debe ser mayor o igual a la
capacidad de carga a la tracción de la rosca macho.
Donde:
F = Fuerza axial sobre el tornillo.
At = Área de tracción de la rosca macho.
Rm = Resistencia a la tracción del
material de fabricación del tornillo o rosca macho.
La misma fuerza “F” se aplica sobre la rosca, de manera que
tenemos:
Donde:
F = Fuerza axial sobre el tornillo.
Ac1 = Área de corte unitaria de la rosca
hembra. Ecuación [7.1].
t
= Resistencia al corte del material de fabricación de la rosca hembra.
De acuerdo a la bibliografía sobre
resistencia de materiales la relación que hay entre la resistencia a la
tracción (Rm) y la resistencia al corte (t) en los aceros es:
t »
Rm x (0,5 a 0,65)
Que en nuestro caso tomamos la peor
condición, t =
0,5 x Rm.
Igualando [8] y [9] y despejando “L” tenemos la relación
que nos permite determinar la longitud roscada de enganche que cumple con la
condición enunciada.
Esta ecuación es válida para tornillos y tuercas del mismo material, es decir con la misma resistencia a la tracción.
Por ejemplo, tornillo y tuerca fabricados con acero SAE 1045.
Cuando los materiales son diferentes en cuanto a la
resistencia a la tracción la fórmula [10] toma la expresión:
Donde:
L = Longitud roscada de enganche.
At = Sección de tensión a la tracción
del tornillo.
Ac1 = Área de corte unitaria [7.1] de la
rosca hembra.
Rmm = Resistencia a la tracción del
acero de la rosca macho.
Rmh = Resistencia a la tracción del
acero de la rosca hembra.
La sección de tensión a la tracción del tornillo está en
las tablas de roscas y se estima por:
Donde:
At = Sección de tensión a la tracción
del tornillo.
d = diámetro nominal de la rosca macho.
P = Paso de la rosca.
Debo aclarar que las fórmulas [10] y [11] son para roscas
de acero. Para otros materiales, el factor “2” cambia según sea el caso.
La tabla siguiente da unos valores de referencia entre la tensión
de corte y la tensión de tracción de algunos materiales según la VDI 2230.
|
Material
|
Relación corte/tensión
|
|
t/Rm
|
|
|
Aceros
|
0,60 a 0,65
|
|
Acero Austenítico
|
0,80
|
|
A. Austenítico F60/90
|
0,65 a 0,75
|
|
Fundiciones GJL
|
1,1
|
|
Fundición GJS
|
0,9
|
|
Aluminio aleado
|
0,7
|
|
Aleaciones de titanio
|
0,6
|
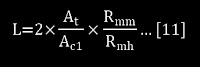
Las fórmulas [10] y [11] expresan la longitud roscada de
enganche para la condición en que la rosca hembra soporta la misma carga que el
núcleo del tornillo. Como norma debe aplicarse un factor de seguridad (que
establece el usuario) a la longitud calculada para ir seguros sobre la
resistencia de la rosca hembra.
Podemos hacer el mismo análisis anterior para la rosca
macho, en cuyo caso la sección sometida a corte del filete de la rosca se
determina por:
Donde:
Act = Área o sección de corte del filete
de la rosca macho.
P = Paso.
Dmax = Diámetro interno máximo de la
rosca hembra.
d2max = Diámetro primitivo máximo de la
rosca macho.
L = Longitud roscada de enganche.
Hay que recordar que las fórmulas requieren unidades
coherentes para que los resultados sean coherentes.
El siguiente ejemplo nos permite verificar el uso de la
fórmula para determinar la longitud roscada de enganche.
Un tornillo M36x4 – 10.9
sometido a una carga de 63.000 Kg está roscado a una pieza de acero SAE
1022. Determinar la longitud roscada de enganche adecuada. Tolerancia de
fabricación de las roscas 6g/6H.
Tornillo M36x4 - 6g -
10.9:
Paso = 4 mm.
dmin = 35,47 según norma DIN 13.
Rmm = 104 Kg/mm2. (10.9)
At = 816,7 mm2 según [12]
Rosca hembra:
Paso = 4 mm.
D2max = 33,7 mm (DIN 13).
Rmh = 43 Kg/mm2. (SAE 1022).
Ac1 = 84,19 mm2 Según [7.1]
De acuerdo a la fórmula [7] podemos determinar la longitud
de enganche “L” necesaria para que la rosca hembra soporte la carga. Partiendo
de la tensión de corte del filete de la rosca:
Despejando “L” de [7], tenemos:
L = 34,8 mm
Esta es la longitud roscada de enganche mínima necesaria
para que la rosca hembra soporte la carga de rotura, sin embargo bajo esta condición
el tornillo es capaz de soportar una carga de rotura de »85 toneladas como lo indica la
formula siguiente, lo que implica que fallaría primero la rosca hembra si la
unión fuese sometida a esta carga.
Como la condición requerida es que la rosca hembra sea la
más resistente (es más fácil reponer la rosca macho que la rosca hembra) y
tratándose de aceros diferentes para la rosca macho y la rosca hembra aplicamos
la fórmula [11].
Este resultado de 45 mm es la longitud roscada mínima de
enganche requerida para que se cumpla la condición de que la rosca hembra
soporte la misma carga de rotura que el tornillo, no obstante al resultado hay
que aplicarle un factor de seguridad, por ejemplo de 1,5.
L = 1,5x45 = 67,5 mm
Esta es la
longitud roscada de enganche requerida. L = 67,5 mm
Si la pieza a sujetar posee un espesor de 90 mm, nuestro
tornillo de fijación debería de tener una longitud de 157,5 mm (90+67,5). La
longitud normalizada de los tornillos más cercana a la estimada es de 160 mm
con lo cual emplearíamos un tornillo M36x4x160 -10.9 con acabado de fabricación
medio 6g.
Espero que con esta corta explicación haya cubierto algunas
inquietudes con respecto a la resistencia mecánica de las roscas.






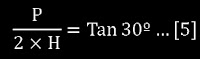



Me salvaste la vida con tu artículo, hermano...
ResponderBorrarGracias.
Me alegra mucho saberlo.
BorrarPersonas como tú nos ayudan a mejorar nuestra calidad profesional, gracias
BorrarEstimado me podrías dar la bibliografía empleada.
ResponderBorrargracias muy buen articulo
La mayoría de los textos de mecánica a nivel universitario sobre el tema dan la información o parte de ella. Las explicaciones que aparecen en la norma VDI 2230 son muy buenas y las fórmulas aparecen en el apéndice de la norma ASME B1.1-2003.
BorrarGracias por la visita
Entiendo que la rosca no toma uniformemente la carga, Tengo la idea, pero no he podido encontrar sustento, que las tres primeras espiras soportan alrededor del 70% de la carga
BorrarHola, Fernando! Muy bueno su post! Felicitaciones!
ResponderBorrarQuisiera saber de dónde puedo sacar la tabla DIN13.
Gracias y felicitaciones.
Saludos
Excelente Articulo, muchas gracias.......
ResponderBorrarExcelente Artículo Compañero. Muchas Gracias!
ResponderBorrarGracias por la visita
BorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarexcelente.
ResponderBorrarhola. por favor su ayuda... existe alguna norma donde se indique que la rosca de la tuerca debe ser cubierta al 100% en su longitud por la rosca del perno...??? Un constructor quiere colocar un conector de puesta a tierra pero el perno es muy corto y no cubre la totalidad de la rosca de la tuerca.
ResponderBorrarComo ejemplo, la norma alemana DIN 78. Allí aparece tu consulta, incluso de acuerdo al "tipo" de tuerca, es decir gruesa, almenada, delgada... etc.
BorrarToda la tuerca y sobresalir un poco.....
Gracias por la visita.
¿Puedes decirme qué bibliografía has empleado? Me gustaría consultarla, gracias.
ResponderBorrarMuy buen aporte, pero solo tengo una duda tendras el depeje de L de la ecuacion numero 7 ??Te lo agradeciria muchimo o algien mas que la pudiera publicar seria genial
ResponderBorrarL=Ac x P/(pi x dmin x [lo que está dentro del corchete])
BorrarDisculpa que no muestre la ecuación completa, pero escribirla acá es un poco latoso.
Gracias por la visista.
Excelente aporte estimado. Muy agradecido
ResponderBorrarSolo me queda preguntar por la biblografia usada algo que respalde las formulas usadas.
ResponderBorrarNo se si estoy equivocado pero el diámetro menor o interno Según DIN 13 es d3= 31,09 y el diámetro medio o primitivo es D2= 33,4 y no d3= 35,47 y D2= 33,7 respectivamente. Tan bien el calculo de longitud roscada es mas sencillo con la formula L= 2x At/Ac1. De todas formas muy bueno su aporte gracias.
ResponderBorrarEste comentario ha sido eliminado por el autor.
Borrarte dejo el link para que veas las tablas https://www.tormetal.com/wp-content/uploads/2017/04/6-TMT-CAT-FIX-AP-Tecnico-Roscas.pdf
Borrarpero de tu formula, queda área * área, lo cual hace una medida adimensional, o hay algo que se me está yendo?
BorrarBuenos días,
ResponderBorrar¿Cómo es posible que de la ecuacion (11) obtengamos milímetros cuando estás dividiendo Área entre Área y resistencia entre resistencia,
L=2x(At/Ac1)*(Rmm/Rmh); At/Ac=adimensional ; Rmm/Rmh=adimensional;
¿DE DÓNDE SALEN LOS MILÍMETROS?
Recuerda que Ac1 es el área de corte por mmm de recorrido (área de corte unitario), de manera que sus unidades son mm2/mm.
BorrarGracias por tus comentarios.
Yo igual estoy tratando de resolver esa duda, 3 años despues de ti, encontre otra formula similar en la cual se obtiene la distancia pero al final igual queda adimensional, lo resolviste de alguna forma?
BorrarTiene alguna forma de aclararme por favor lo de el área de corte unitario?, respecto a las unidades me encuentro en ese dilema igualmente y no logro resolverlo
BorrarDe la ecuación (9) tampoco es posible obtener fuerza:
ResponderBorrarF=Ac1*L*t;
Ac1: (mm2)
L: (mm)
t: N/mm2
Si multiplicas todo, las unidades del resultado final son N*mm, lo que se corresponde con unidades de PAR, no de FUERZA
Muchas gracias por tu aporte, muy bueno y la claridad con que lo hiciste!!
ResponderBorrarGracias por la visita
BorrarSaludos estimado que opinas de conectar un motor de corriente alterna de 50Hz en la red de 60 Hz
ResponderBorrarEn realidad no ocurre nada grave…. Un aumento del 10% en las rpm y en la potencia…..
BorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarHola, primero de todo excelente documento, me está ayudando mucho.
ResponderBorrarTengo una duda sobre el cálculo, si el macho es hueco por dentro (es un tubo), ¿Cómo se podría calcular para tener en cuenta este hueco o llegar a determinar el espesor de pared necesario? ¿Se podría restar el área interior al área de sección de corte?
Muchas gracias de antemano
Gracias por la visita. En este caso es así de fácil, restas el área interior y aplicas las fórmulas.
Borrarhola, tengo una pregunta, si el tornillo es prisionero y el material donde rosca es de aluminio, que norma me sirve para realizar ese análisis.
ResponderBorrarEl cálculo lo realizas de acuerdo a la resistencia del aluminio empleado.
Borrarme urge contactar al autor alsh94_@hotmail.es es mi correo
ResponderBorrarBuenas tardes, la ecuación [13] está mal, el interior del parántesis sería (d2max-Dmax) en vez de (Dmax-d2max).
ResponderBorrarUn saludo.